Beginning Python
Python is a programming language which allows us to give instructions to the computer. These instructions can be as simple as "add together these two numbers" or as complex as "give me the average CO2 concentration for 2020". For the former we will be able to complete the task using only a single instruction but for the latter, we may have to write a larger program containing hundreds or thousands of instructions.
This course is going to start from the beginning, showing you to talk to the computer to perform simple tasks and as you become more confident and follow the later courses, you will find that you are able to write much more complex programmes.
Python is a well-established language, with the current version (version 3) released in 2008 and it is installed by default on nearly all modern Linux systems. Python is also available for MacOS and Windows.
This workshop is going to introduce you to the basics of the Python programming language with more advanced topics being covered by later workshops.
You can jump ahead to any chapter:
Setting up your workspace¶
There are lots of different ways to run Python code and many tools to help you write it. You don't require any special tools to create a Python script, a simple text editor like Notepad on Windows is sufficient. More advanced tools include things like Jupyter Notebooks and IDEs like PyCharm or Visual Studio Code.
For this workshop we will be keeping things as simple as possible in order to allow us to focus on the topics we're learning without having to learn too many extra tools along the way.
For the purpose of this course we will be using a free tool called JupyterLab which provides you with a local editor in your web browser where you can write and run Python code. The easiest way to get access to JupyterLab is to install Anaconda which is a piece of software which includes Python along with lots of other tools. It is freely available for Windows, MacOS and Linux.
Anaconda can be installed into your home area on your computer so if you are on a work laptop, for example, you will not need any special permissions. Once Anaconda is installed, start "Anaconda Navigator" and press the JupyterLab button on the main screen:
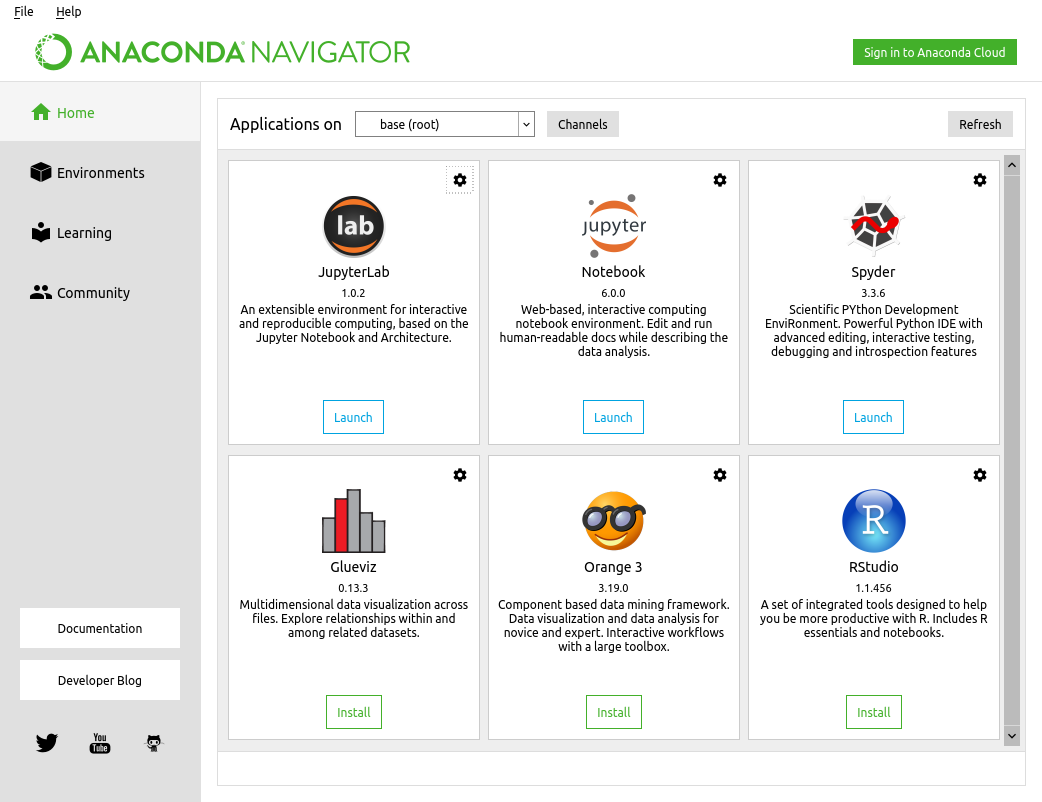
This will open JupyterLab in your default web browser and will look something like this:
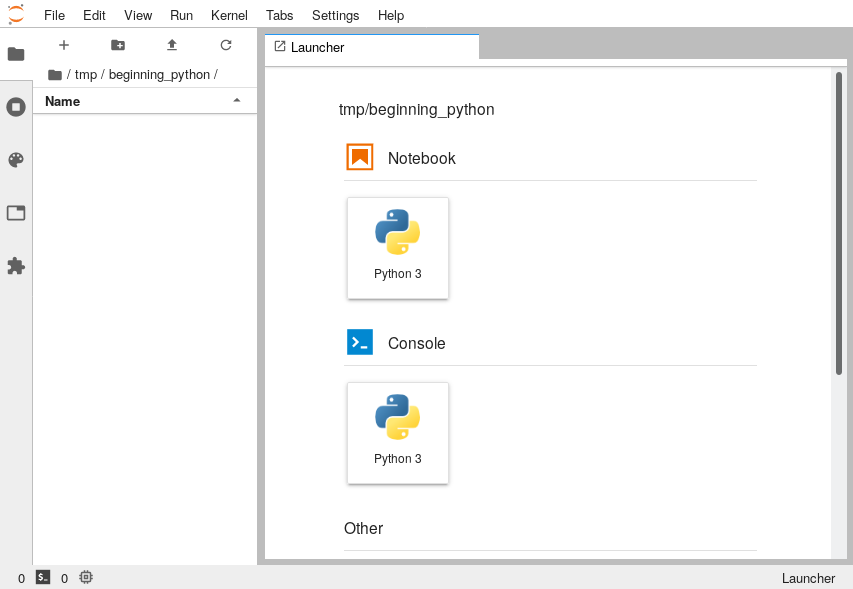
The way that we will be setting up the space is to have a text editor on the left-hand side of the screen and a terminal on the right hand side. We'll use the editor to write our code and the terminal to run it.
In the launcher tab, scoll down to the "Text File" entry and click that. It will turn the editor into a text editor. Then go to File → New and select "Terminal". It will now have two tabs inside the interface, one labelled "untitled.txt" and the other labelled "Terminal 1":
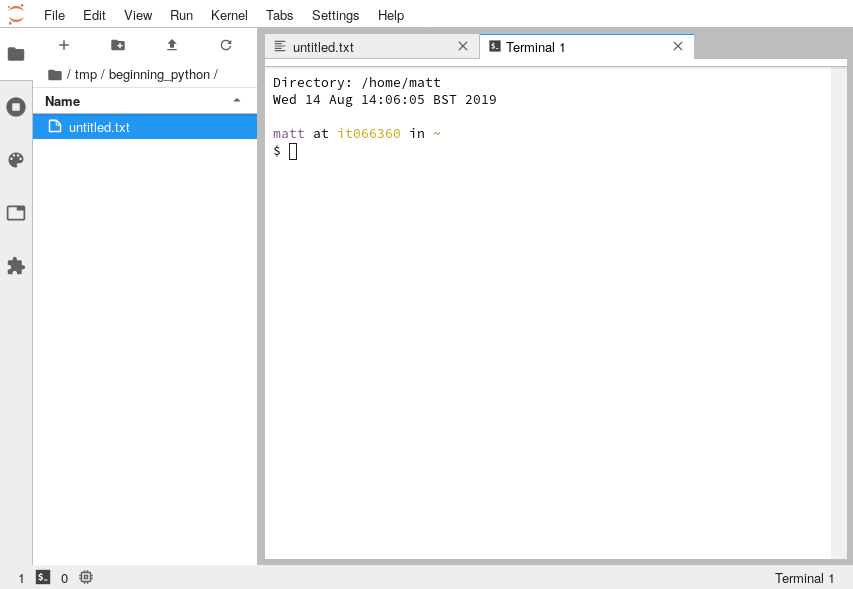
The contents of the Terminal tab will likely be a little different on your computer, compared to what is shown in thise images but that is ok.
To make our lives easier, let's rearange things so that we can see the text editor at the same time as the terminal. Do this by pressing and holding down the left mouse button on the tab that says "Terminal 1" and slowly dragging it to the right-hand side of the window. You'll see a blue outline like this:
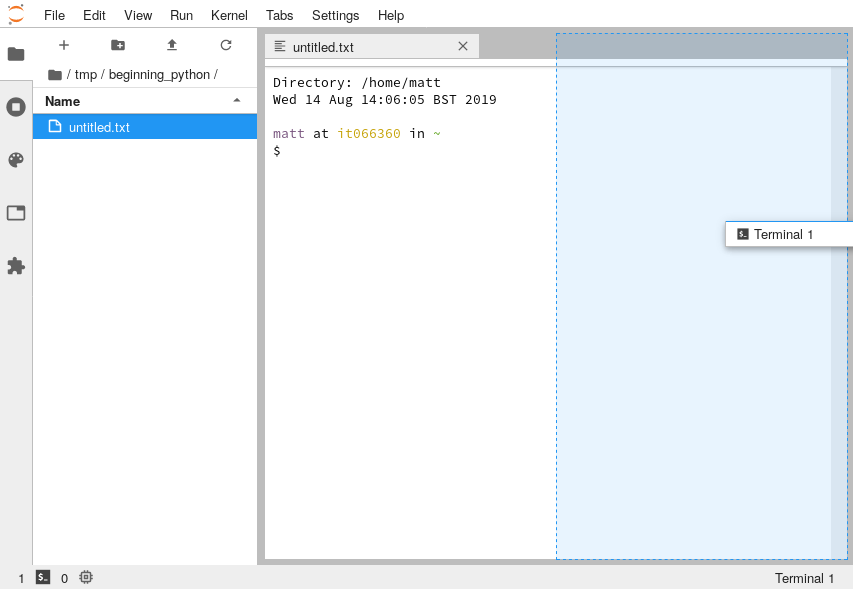
Release the mouse button and you'll end up with the two showing side-by-side:
We're now ready to get started!